解题思路:
基础代码:
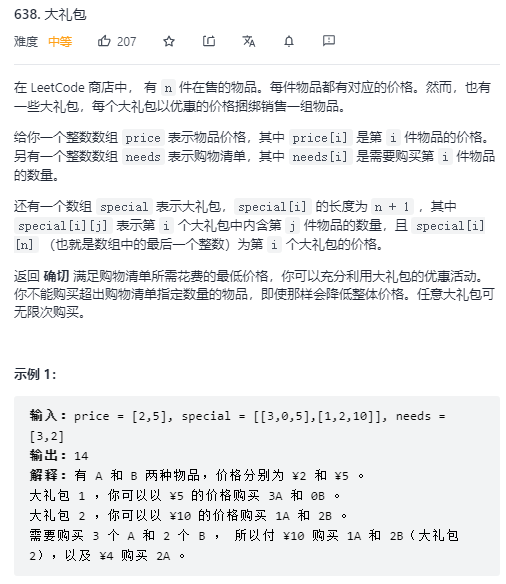
近期花时间比较长的一道题,一开始以为是动态规划的题目,后面发现思路走不通换成DFS的思路。主要还是通过深搜+剪枝来获取所有可能的情况,而后通过min()来获取其最小值。
- 用minPrice来作为最小值的记录,在最外层for循环结束(即当前层级的所有可能性结束后)返回
- 记录下lastPrice,其作为递归向下寻找可能性的依据,需要作为参数单独传入dfs函数中,一开始是把minPrice传进去,思路肯定是不对的(这样的话totalPrice就没办法保存下来了)。
- 记录下curPackagePrice,表示当前购买礼包所花费的价钱,根据其和needs计算后续的总价格totalPrice。
- 在每次循环过后要对needs和curPackagePrice进行还原
- 注意:minPrice仅代表当前DFS层级上的最小价格。
以下为C++代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| class Solution {
public:
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter = RemovePackages(price, special, needs);
int lastPrice=0;
for(int i=0;i<needs.size();i++){
lastPrice+=needs[i]*price[i];
}
return dfs(price, filter, needs,0,lastPrice);
}
vector<vector<int>> RemovePackages(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter;
for (int i = 0; i < special.size(); i++) {
int temp = 0;
for (int j = 0; j < special[0].size() - 1; j++) {
temp += price[j]*special[i][j];
}
if (temp > special[i].back()) {
filter.push_back(special[i]);
}
}
return filter;
}
int dfs(vector<int>& price, vector<vector<int>>& filter, vector<int>& needs,int curPackagePrice,int lastPrice) {
int totalPrice = 0;
int minPrice = lastPrice;
for (int i = 0; i < filter.size(); i++) {
bool succ = true;
totalPrice = 0;
for (int j = 0; j < filter[i].size() - 1; j++) {
if (needs[j] < filter[i][j]) {
succ = false;
break;
}
}
if (!succ) continue;
else {
curPackagePrice += filter[i].back();
totalPrice += curPackagePrice;
for (int j = 0; j < needs.size(); j++) {
needs[j] -= filter[i][j];
totalPrice += needs[j] * price[j];
}
}
minPrice = min(minPrice,dfs(price, filter, needs,curPackagePrice,totalPrice));
for (int j = 0; j < filter[i].size()-1; j++) {
needs[j] += filter[i][j];
}
curPackagePrice -= filter[i].back();
}
return minPrice;
}
};
|
优化过程:
△发现还是有可优化的点,可以把curPackagePrice和lastPrice去掉
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| class Solution {
public:
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter = RemovePackages(price, special, needs);
return dfs(price, filter, needs);
}
vector<vector<int>> RemovePackages(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter;
for (int i = 0; i < special.size(); i++) {
int temp = 0;
for (int j = 0; j < special[0].size() - 1; j++) {
temp += price[j]*special[i][j];
}
if (temp > special[i].back()) {
filter.push_back(special[i]);
}
}
return filter;
}
int dfs(vector<int>& price, vector<vector<int>>& filter, vector<int>& needs) {
int minPrice = 0;
for(int i=0;i<needs.size();i++){
minPrice+=needs[i]*price[i];
}
for (int i = 0; i < filter.size(); i++) {
bool succ = true;
for (int j = 0; j < filter[i].size() - 1; j++) {
if (needs[j] < filter[i][j]) {
succ = false;
break;
}
}
if (!succ) continue;
else {
for (int j = 0; j < needs.size(); j++) {
needs[j] -= filter[i][j];
}
}
minPrice = min(minPrice,dfs(price, filter, needs)+filter[i].back());
for (int j = 0; j < filter[i].size()-1; j++) {
needs[j] += filter[i][j];
}
}
return minPrice;
}
};
|
附带上官方题解的记忆化深搜
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| class Solution {
public:
map<vector<int>, int> memo;
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
int n = price.size();
vector<vector<int>> filterSpecial;
for (auto & sp : special) {
int totalCount = 0, totalPrice = 0;
for (int i = 0; i < n; ++i) {
totalCount += sp[i];
totalPrice += sp[i] * price[i];
}
if (totalCount > 0 && totalPrice > sp[n]) {
filterSpecial.emplace_back(sp);
}
}
return dfs(price, special, needs, filterSpecial, n);
}
int dfs(vector<int> price,const vector<vector<int>> & special, vector<int> curNeeds, vector<vector<int>> & filterSpecial, int n) {
if (!memo.count(curNeeds)) {
int minPrice = 0;
for (int i = 0; i < n; ++i) {
minPrice += curNeeds[i] * price[i];
}
for (auto & curSpecial : filterSpecial) {
int specialPrice = curSpecial[n];
vector<int> nxtNeeds;
for (int i = 0; i < n; ++i) {
if (curSpecial[i] > curNeeds[i]) {
break;
}
nxtNeeds.emplace_back(curNeeds[i] - curSpecial[i]);
}
if (nxtNeeds.size() == n) {
minPrice = min(minPrice, dfs(price, special, nxtNeeds, filterSpecial, n) + specialPrice);
}
}
memo[curNeeds] = minPrice;
}
return memo[curNeeds];
}
};
|
△查看之后发现自己上面的那种方法还是会出现重复计算的情况,没有去应用到记忆化的目的,还是再跟着思路去敲一遍。
稍微简化了一下题解的记忆化深搜:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| class Solution {
public:
map<vector<int>,int> memo;
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter = RemovePackages(price, special, needs);
return dfs(price, filter, needs);
}
vector<vector<int>> RemovePackages(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
vector<vector<int>> filter;
for (int i = 0; i < special.size(); i++) {
int temp = 0;
for (int j = 0; j < special[0].size() - 1; j++) {
temp += price[j]*special[i][j];
}
if (temp > special[i].back()) {
filter.push_back(special[i]);
}
}
return filter;
}
int dfs(vector<int>& price, vector<vector<int>>& filter, vector<int>& needs) {
if(!memo.count(needs)){
int minPrice = 0;
for(int i=0;i<needs.size();i++){
minPrice+=needs[i]*price[i];
}
for (int i = 0; i < filter.size(); i++) {
bool succ = true;
for (int j = 0; j < filter[i].size() - 1; j++) {
if (needs[j] < filter[i][j]) {
succ = false;
break;
}
}
if (!succ) continue;
else {
for (int j = 0; j < needs.size(); j++) {
needs[j] -= filter[i][j];
}
}
minPrice = min(minPrice,dfs(price, filter, needs)+filter[i].back());
for (int j = 0; j < filter[i].size()-1; j++) {
needs[j] += filter[i][j];
}
}
memo[needs]=minPrice;
}
return memo.count(needs);
}
};
|
最后也算优化到比较好的情况: