1218. 最长定差子序列

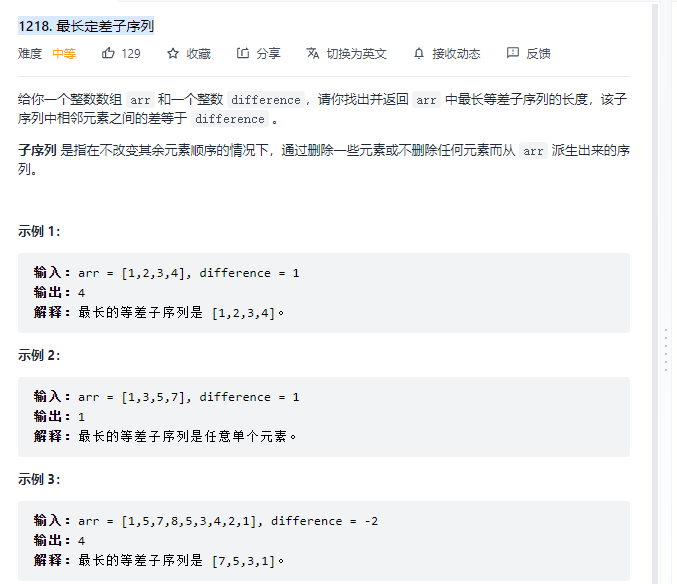
image-20211105194905197

解题思路：

​ 这题是动态规划的题目，其实往深了看可以作为一个背包问题，arr中元素为每件物品的权重，而等差数列则是每件物品权重判断的条件，在内部将背包问题中的max()求最大存储物品数量改为等差数列长度+1。

方法思路：

  • map第一个元素表示符合等差数列的最后一个元素，第二个表示该等差数列的长度
  • 遍历arr的元素，若m不存在则加入其中，若存在则获取其长度后+1赋值给当前元素对应值

以下为C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        //动态规划
        //第一个元素表示符合等差数列的最后一个元素，第二个表示该等差数列的长度
        //遍历arr的元素，若m不存在则加入其中，若存在则获取其长度后+1赋值给当前元素对应值
        unordered_map<int,int> m;
        for(auto num:arr){
            m[num]=m[num-difference]+1;
        }

        //找最大长度
        int res=0;
        for(auto iter=m.begin();iter!=m.end();iter++){
            res=max(res,iter->second);
        }
        return res;
    }
};