375. 猜数字大小 II

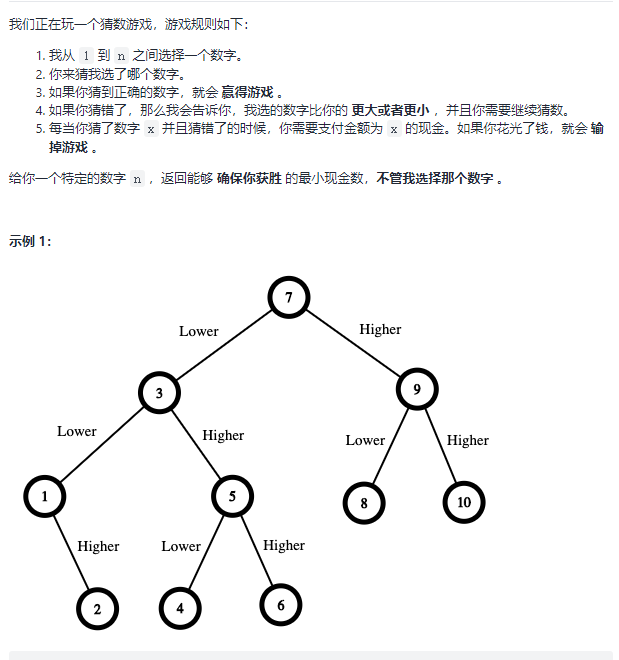
image-20211112102250370

解题思路：

​ 动态规划的题目，太久没做类似的了没找到合适的思路，后面查看题解后发现能以dp[i][j]表示猜由i到j数的最小现金数。（可以将题目类比为背包，最小金额–最大价值，货物种类&&背包容量–猜数范围）

  • 递推式子在每次确定范围后为max(dp[k+1][j],dp[i][k-1])，因为要保证确保获胜，所以要取max。
  • 当dp[i][i]时，不用支付现金，因此dp[i][i]=0
  • 外层i确定每次遍历左边界，外层j确定每次遍历右边界，因为初始化时已经让dp中所有元素都为0，所以外层遍历直接保证i!=j即可，无需重复赋值0
  • 根据范围遍历范围内所有可能的猜数情况，根据递推式求出各个情况的保证获胜的最小金额数，将其最小值赋值给dp[i][j]

以下为C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int getMoneyAmount(int n) {
         //动态规划问题，最小现金数可以类比为背包问题中的最大价值
        //设定dp[i][j]为从i到j中猜数所需要的支付的最小现金数
        //递推式子在每次猜数遍历后为min(dp[x+1][j],dp[i][x-1])+x;

        //初始化数组(或者用vector来存储)
        int** dp = new int* [n + 1];
        for (int i = 0; i <= n; i++) {
            dp[i] = new int[n + 1]();
        }

        //vector<vector<int>>(n+1,vector<int>(n+1));

        for (int i = n; i > 0; i--) {
            for (int j = i+1; j <= n; j++) { 
                //找到在对应范围内的最小现金数
                int min_cost = INT_MAX;
                for (int k = i; k < j; k++) { 
                    int cost = max(dp[k + 1][j], dp[i][k - 1]) + k;//为了保证在所有情况下都能获胜，应考虑最坏情况
                    min_cost = min(min_cost, cost);
                }
                dp[i][j] = min_cost;
            }
        }

        return dp[1][n];
        
    }
};